Luku 2.4: Tehtävä: Social Networking

Tästä sivusta:

Pääkysymyksiä:

Mitä käsitellään? Yksikkötestaus jatkuu.

Mitä tehdään? Ohjelmoidaan yksinkertainen algoritmi.

Suuntaa antava vaativuusarvio: Keskivaikea

Suuntaa antava työläysarvio: 1-2 tuntia

Pistearvo: S100

Bonus: +5 % omista pisteistä aikaisesta palautuksesta.

Vinkki

current = self #most-recent holder

Jos et ymmärrä mitä self tarkoittaa yksinään, ota selvää (se helpottaa tehtävän tekoa).

Intro

Social networking sivustoilla kuten Facebook, LinkedIn ja MySpace on miljoonia käyttäjiä. Verkoston solmut ovat käyttäjiä tai yhteisöjä, joiden välillä on jonkinlaisia yhteyksiä. Sivuston käyttäjänä voit vaikka tutkia ketkä ovat kaveriesi kavereita, tms.

Eräänä päivänä Teemu Teekkari saa mielestään loistoidean. Kehitetään sivusto, joka yksinkertaistaa kaiken äärimmilleen. Sivuston idea on ainoastaan mahdollisimman tehokkasti pystyä selvittämään onko kahden henkilön välillä jonkinlainen ketju. Itse ketju ei Teemua kiinnosta. Tärkeintä on tietenkin että tilaa kuluu mahdollisimman vähän ja algoritmit ovat mahdollisimman nopeita.

Tilankäytön puolesta Teemulla on tiukka vaatimus: Jokaisen henkilön kohdalle saa merkitä vain yhden henkilön jonka k.o. henkilö tuntee. Algoritminkin pitäisi olla tosi tehokas. Onko tämä mahdollista?

Itse asiassa on.

Teemun käyttämä idea perustuu ideaan että tietääksemme että kaksi henkilöä tuntevat toisensa meidän riittää ainoastaan tietää yksi reitti joka yhdistää nämä henkilöt.

Metodi def knows(self, other):
 palauttaa True jos kaksi henkilöä tuntee toisensa.

Ajatellaan että henkilöt on jo ennalta järjestetty niin että jokaiselle sallittu yksi tuttavuussuhde osoittaa jonkinlaisessa kaverien hierarkiassa aina huipulle päin. Seuraamalla kaverijonoa pääsee lopulta huipulle, jossa on yksittäinen kaveri joka ei tunne enää ketään. Sanotaan että hän on kaikkien hänet välillisestikin tuntevien superkaveri. Jos kahdella henkilöllä on yhteinen superkaveri, heidän välillään on tuo aiemmin haluttu yksi reitti.

Metodi def meet(self, other):
 yhdistää kaksi ihmistä jos heidän välillään ei ollut vielä ketjua. Metodi palauttaa True jos kyseessä oli uusi yhteys.

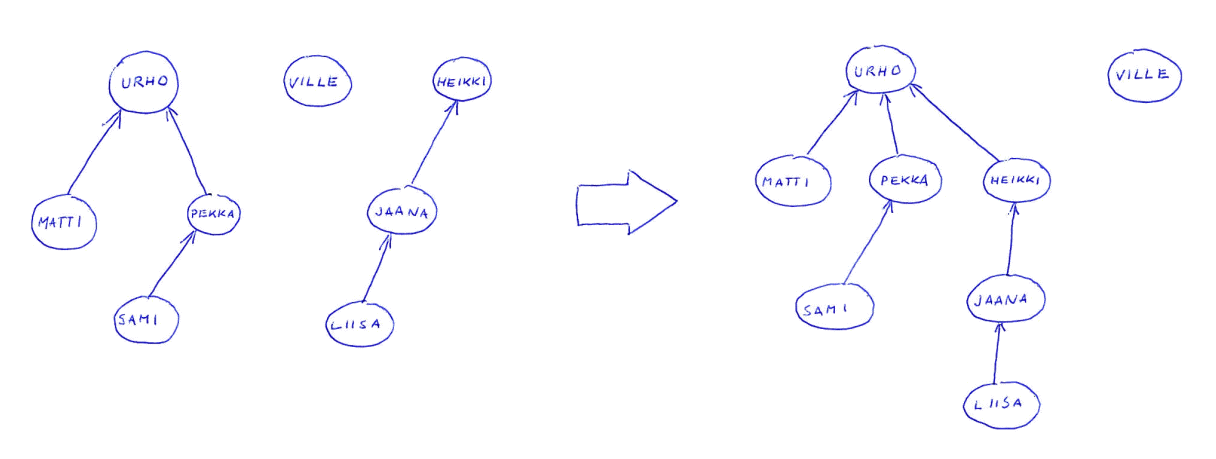
Ok. Jos henkilö A kuuluu kaverien hierarkiaan X ja henkilö B hierarkiaan Y ja he tutustuvat toisiinsa, täytyy kaikkien hierarkioiden X ja Y henkilöiden tuntea toisensa tämän jälkeen. Muistellaanpa... Jos kaksi henkilöä tuntevat toisensa heillä on sama superkaveri. Jotta kaikki X:n ja Y:n ihmiset tuntevat toisensa, heillä pitää siis olla sama superkaveri. Onneksi tämä on helposti hoidettu. Etsitään molempien porukoiden superkaverit ja päätetään että jompikumpi superkavereista tunnustaa toisen kaverikseen. Yksikäsitteisyyden vuoksi päätetään että metodin parametrina annetun henkilön superkaveri on korkeaarvoisempi. (joten muutoksen jälkeen sen friend-kentän arvo on yhä None ja toisen (ex-)superkaverin friend on parametrina annetun henkilön superkaveri.)

Alustusmetodi def _init__(self):
 Aina kun uusi henkilö luodaan, hän on itsessään tällainen kaverien hierarkia - yksittäinen henkilö joka ei tunne ketään. Tämän henkilön superkaveri on hän itse - korkea-arvoisin henkilö jonka hän tuntee. Sama pätee kaikkiin superkavereihin. Huipulla on yksinäistä. Määritellään yksikäsitteisyyden nimissä, että superkaverin kaveri (friend) on None.
../_images/H12t.gif
Esimerkki:

  • (VASEN KUVA) Matin, Pekan ja Samin “superkaveri” on Urho joten nämä neljä tuntevat kaikki toisensa jotakin kautta.

  • (VASEN KUVA) Liisan superkaveri on Heikki. Samin superkaveri on Urho. -> Liisa ja Sami eivät tunne toisiaan.

  • (MUUTOS) Jos tehtäisiin metodikutsu jaana.meet(sami), olisi seuraus kuvassa esitetty muutos. Muutoksessa Jaanan

    superkaveri, Heikki, merkitsee kaverikseen Samin superkaverin Urhon. Tämän jälkeen kaikkien muiden paitsi Villen superkaveri on Urho. Villen superkaveri on hän itse.

Taustoja: Union-Find rakenne

Teemu ei kuitenkaan tehnyt mitään suurta uutta keksintöä vaan sovelsi tunnettua Disjoint Set ADT:n toteutusta. Asiasta kiinnostuneet voivat lukea asiasta Cormen et. al.:in[1] tai Weissin[2] TRAK oppikirjoista.

Jotta rakenne toimisi mahdollisimman tehokkaasti, algoritmiin tehdään yleensä kaksi parannusta. Jos kiinnostaa, voit lukea näistä jommasta kummasta oppikirjasta. Älä toteuta parannuksia tässä harjoituksessa - Webcat-testit on rakennettu olettaen että parannuksia ei ole.

Tehtävänanto

Lue molemmat PyUnit-ohjeet, mikäli et vielä ole lukenut niitä. Halutessasi tee Eclipseen projekti jossa PyUnit:ia on helppo suorittaa.

Tehtävänanto löytyy A+:sta.

Huom!

Muutoksia voi vielä tulla.

Lähdeviitteet

[1] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein, Introduction to Algorithms 2nd ed., MIT Press, 2001

[2] M.A. Weiss, Data Structures and Algorithm Analysis in C, Addison-Wesley Longman Publishing Co., 1997